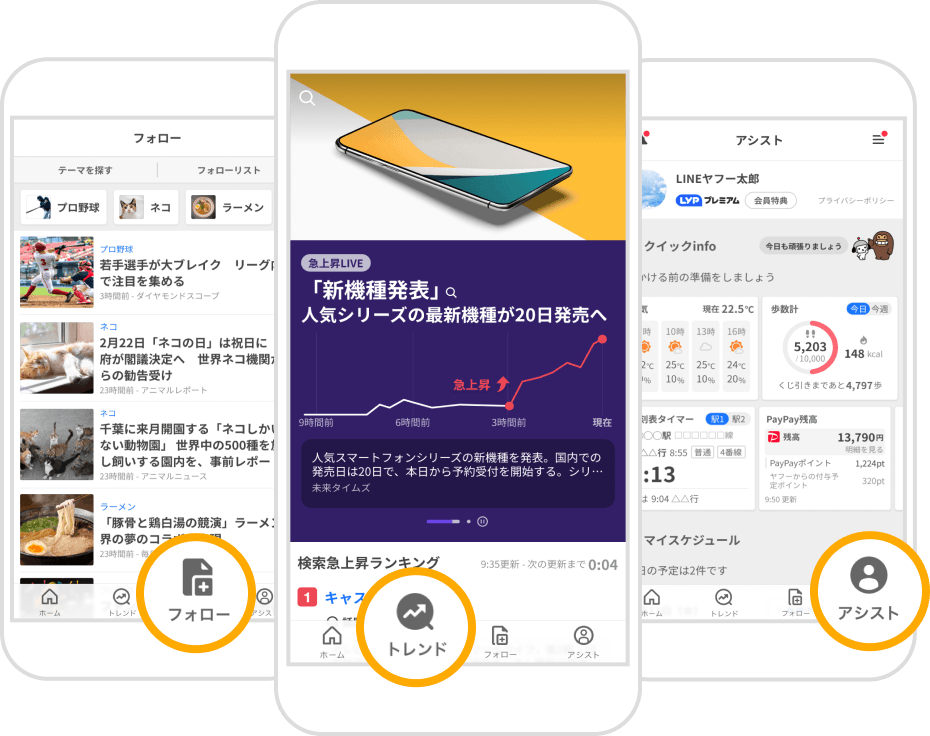
みんなの話題がわかる「トレンド」
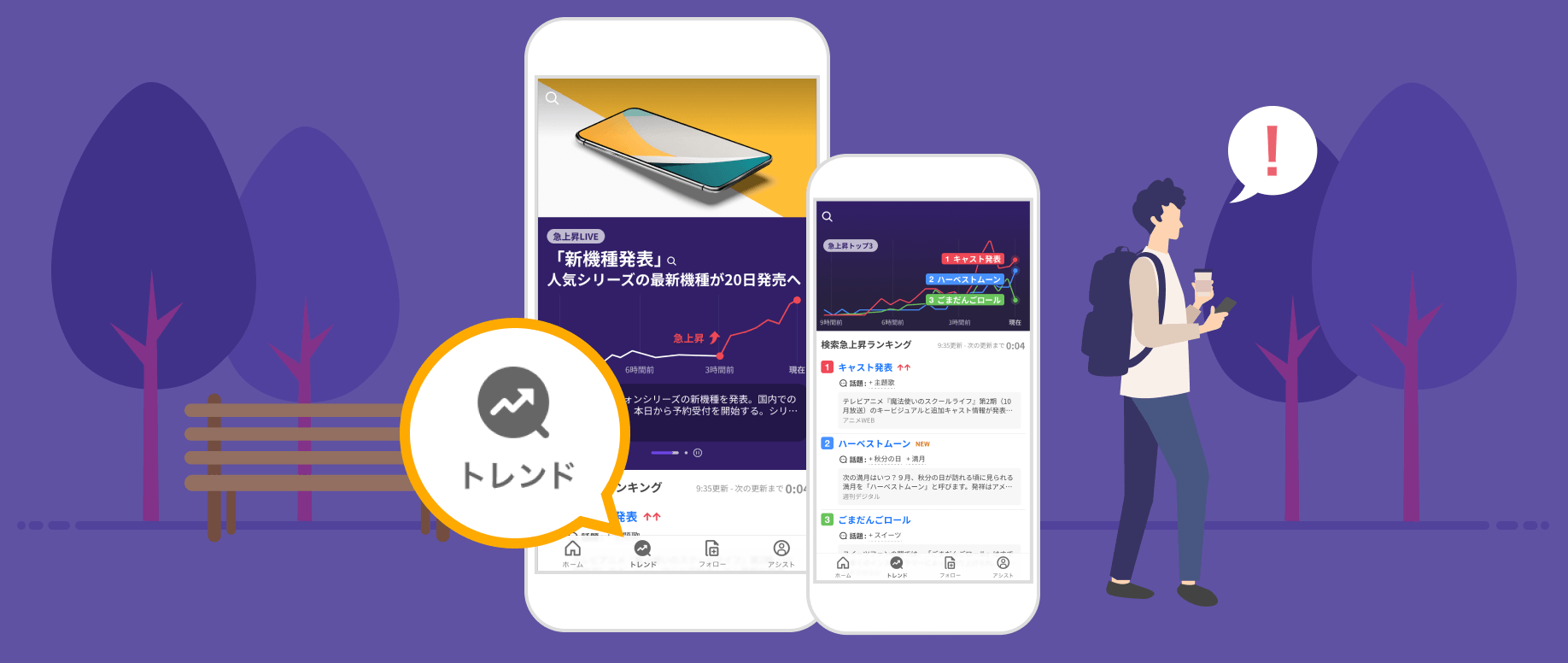
Yahoo!検索の急上昇ワードをランキング化。概要や関連ニュースで「なぜ話題か」もわかります。
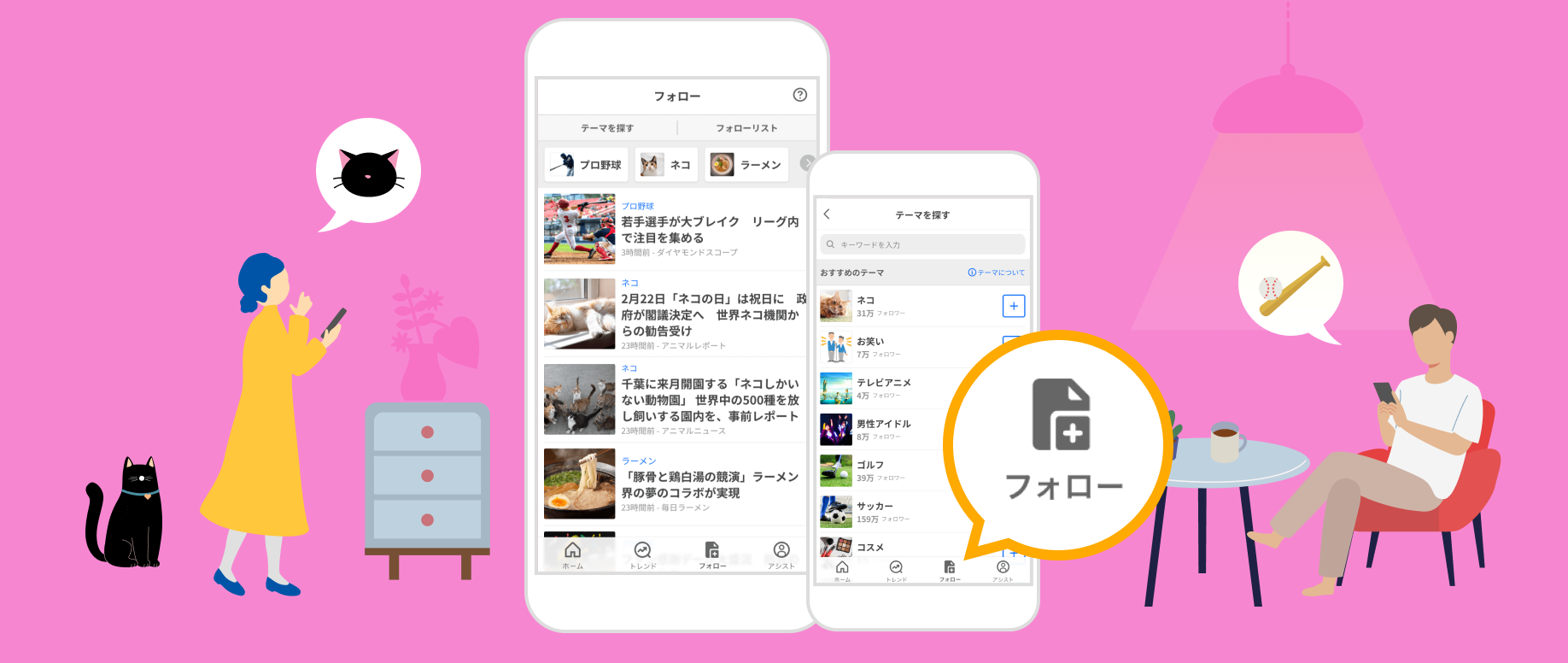
トレンドでできることあなたの興味にこたえる「フォロー」
スポーツや動物、エンタメや経済など、あなたが選んだテーマの最新情報をまとめて確認できます。
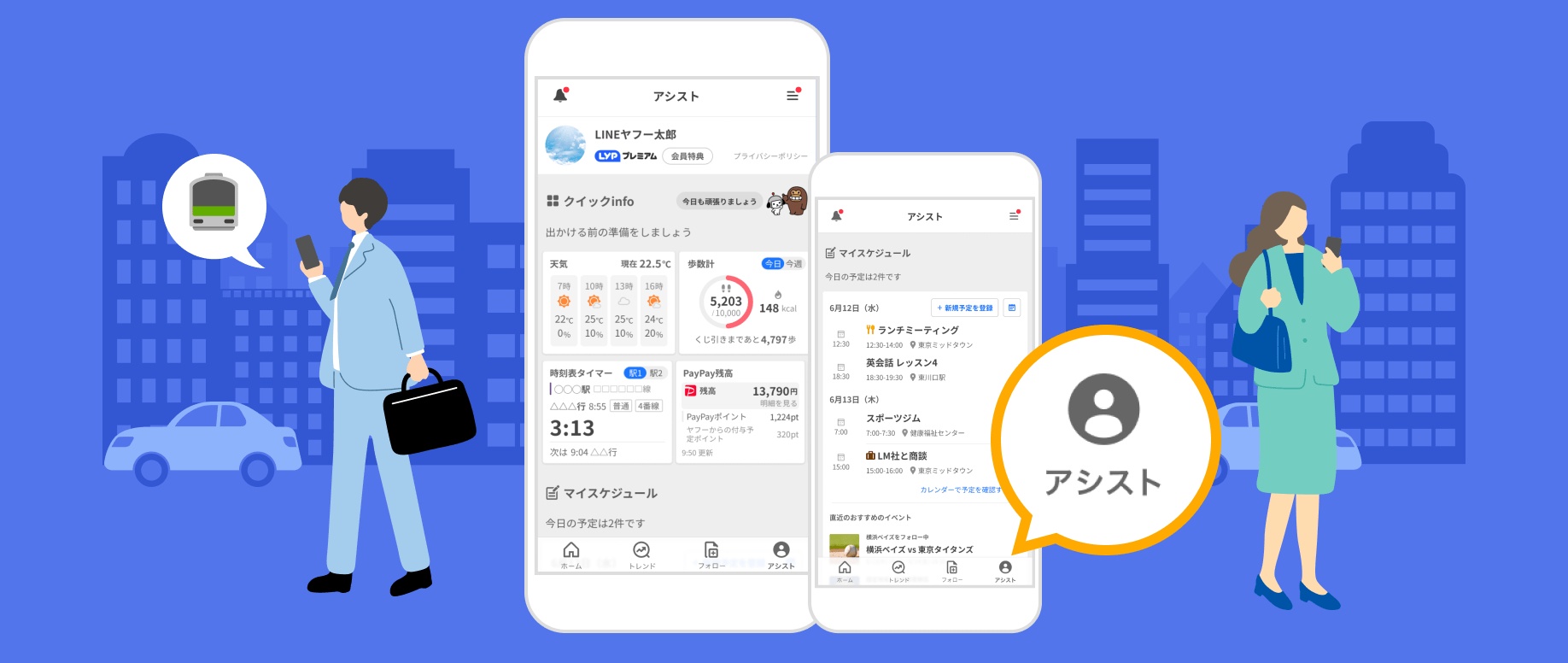
フォローでできることあなたの毎日に役立つ「アシスト」
今日の天気、予定、電車の発車タイマーなど、あなたの1日に役立つ情報を手軽に確認できます。
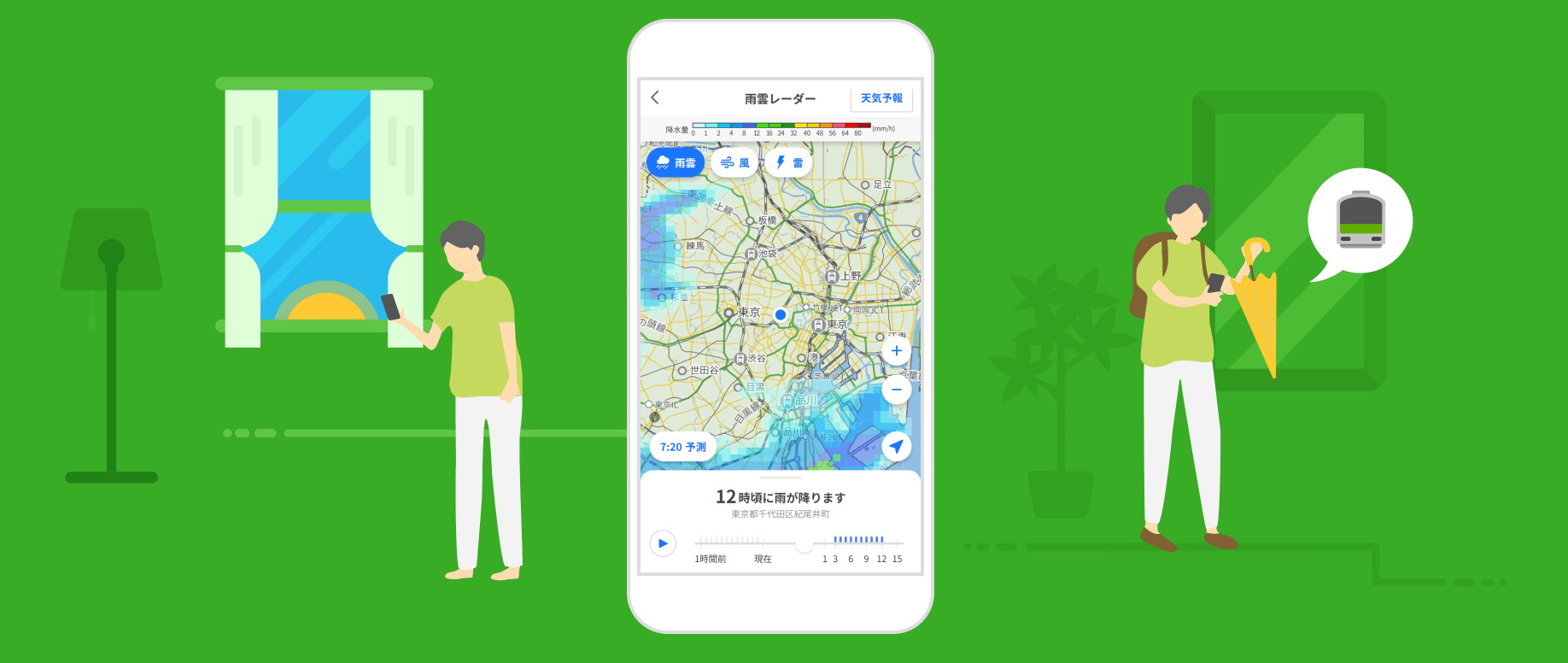
アシストでできること天気や路線をサクッと確認
忙しい外出前の必要情報はこれひとつで。スマートなお出かけをサポートします。
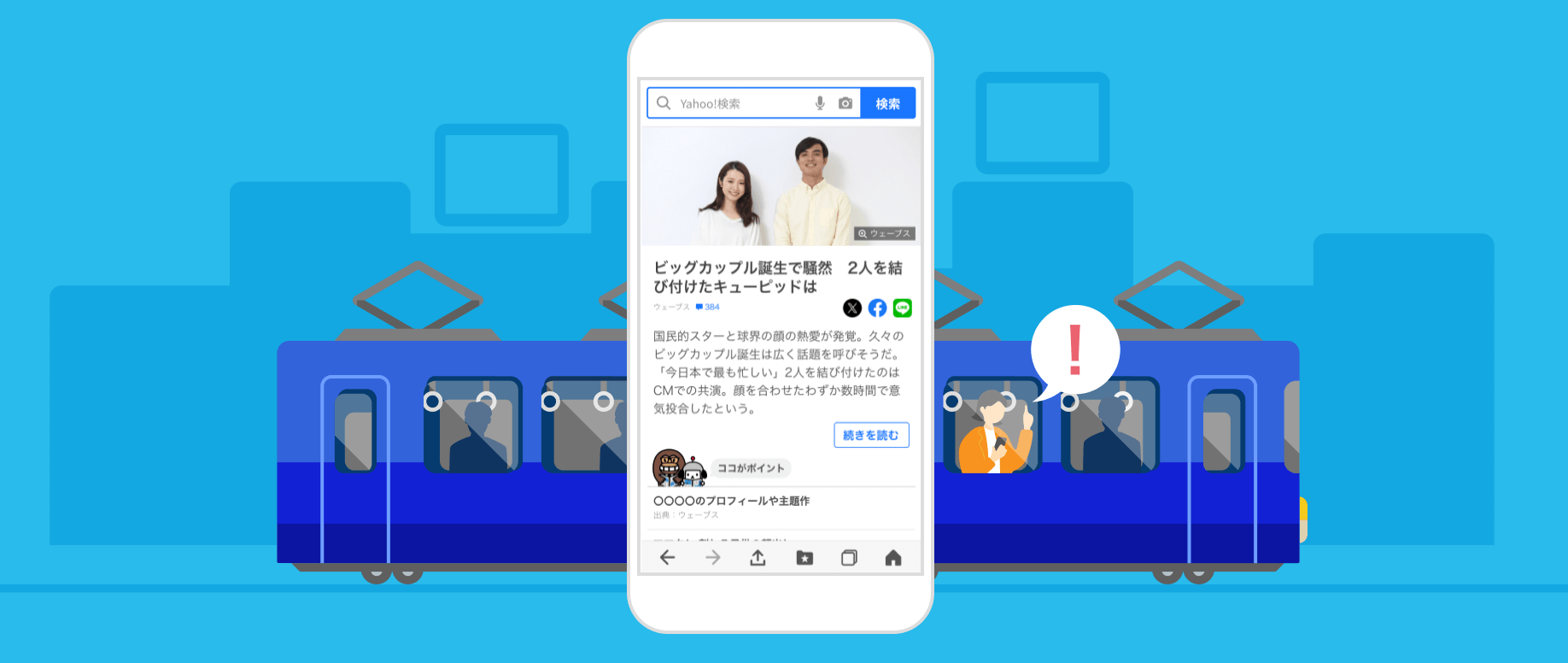
最新のニュースをチェック
最新情報を素早くお届け。気になるワードはその場で検索、深掘りできます。
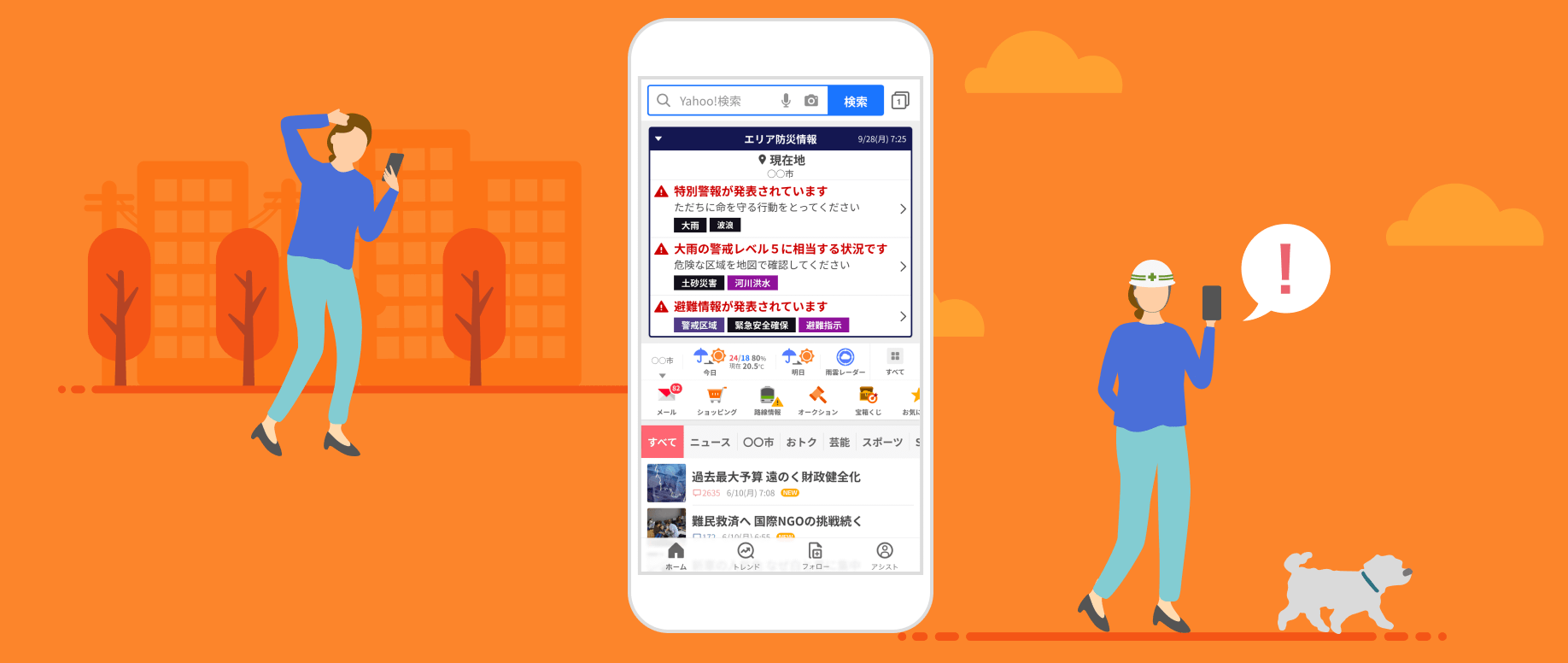
現在地の災害情報を受け取ろう
地震・大雨などの災害・防災情報をPUSHで通知。外出先でもその場の情報を知ることができます。